La regresión logística como discriminadora (diagnóstico y pronóstico)
Desde el punto de vista estadístico, tanto el análisis diagnóstico como el pronóstico, se inscriben en el llamado análisis discriminante, esto es cuando dadas dos muestras pertenecientes a poblaciones distintas y conocida esta pertenencia, determinar el conjunto de variables "descriptoras" (perfil del sujeto) que tiene capacidad de identificar cada una de las poblaciones a las que se hace referencia. Si la pertenencia a cada una de las poblaciones en cuestión la denotamos por los códigos "0 y 1" contenidos en la variable "Y", para el perfil Xβ, podemos escribir:

P(Y = 1˧ |Xβ) = e Xβ/(1 + e Xβ)

Así, dado un perfil X, la idea es determinar si la estimación de probabilidad hecha por la distribución logística está cerca del 0 o cerca del 1. Esta decisión es posible tomarla si se escoge un punto de corte, "p" para la probabilidad estimada, de modo que si P(Y = 1˧ |Xβ) > p, el sujeto será clasificado en la población "1", de lo contrario el sujeto será clasificado en la población "0". Con esta conceptualización, si la población de interés (enfermos, muertes, mejorías…) la llamamos "A" y la codificamos con "1", definimos:

S=P(Y=1 | X ϵ A) : Sensibilidad de la discriminación.

E=P(Y=0 | X ϵ A'): Especificidad de la discriminación.

Obviamente que las probabilidades complementarias definen los sucesos "Falso Negativo" y "Falso Positivo", respectivamente, es decir:

P(Y=0 | X ϵ A) = 1-S: Falso Negativo. (1-S)

P(Y=1 | X ϵ A') =1-E: Falso Positivo. (1-E)

Como nuestro interés es tener buena capacidad de clasificación, es decir, alta sensibilidad y alta especificidad. Lo que se traduce en:

P(Y=1 | X ϵ A)> P(Y=1 | X ϵ A')

S > 1-E

Si la discriminación fuera por azar se tendría S=1-E. Representando gráficamente estas relaciones, donde el eje de las abscisas es 1-E y el de las ordenadas S, se tiene:

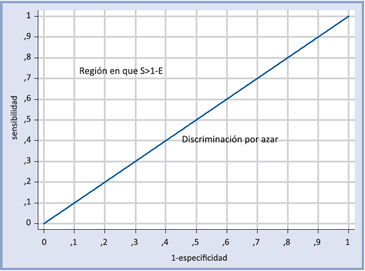
Notar que si la discriminación fuese perfecta, es decir, 100% de sensibilidad y 100% de especificidad, el punto de corte para la discriminación estaría en la intersección de las líneas azules y el área bajo la curva azul sería 1. Obviamente en cualquier aplicación real en que haya buena discriminación, esta área sería menor que 1 pero mayor a 0,5.
Observemos el siguiente ejemplo: Supongamos que la variable X discrimina dos poblaciones, disponemos de 10 valores para la población "1" y 10 valores para la población "0", los datos son los siguientes:

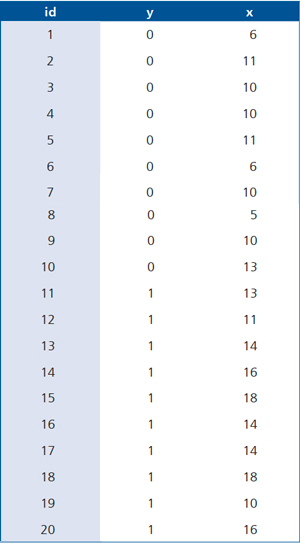
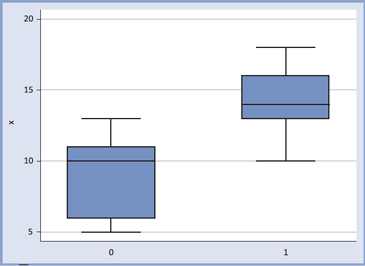
Al ajustar el modelo de regresión logística se obtiene la siguiente salida STATA:

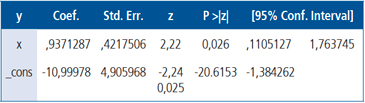
O en términos de la función de probabilidades logística:

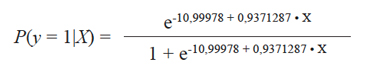
fórmula que al ser evaluada en cada observación entrega las siguientes probabilidades:

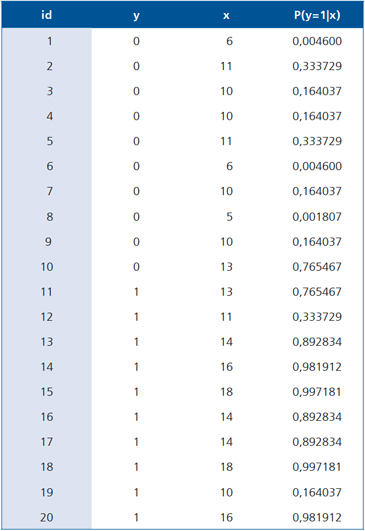
La información anterior la podemos resumir en la siguiente tabla:

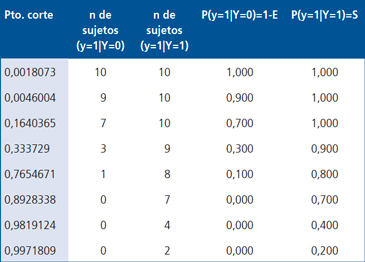
Al graficar la sensibilidad versus 1-especificidad para los distintos puntos de corte se obtiene la curva ROC (Receiver Operating Characteristic).

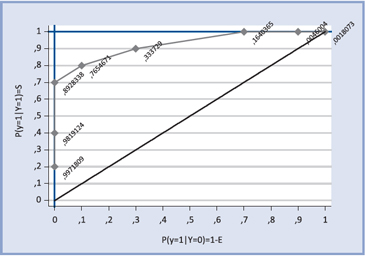
Como se sugirió, la capacidad de discriminación está dada por el área bajo la curva ROC, que en nuestro caso es 0,9250. El mejor punto de corte es aquel que está más cerca de la discriminación perfecta.
Según Hosmer y Lemeshow ("Applied Logistic Regression" Second Edition, p. 162), la capacidad de discriminación puede clasificarse según:

Sin embargo, para encontrar el mejor punto de corte, es preferible usar el siguiente gráfico:

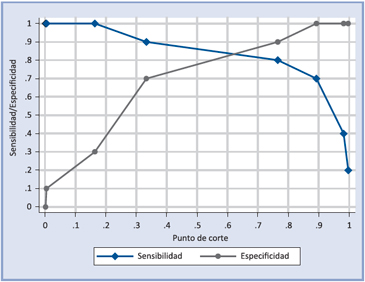
Recordando la definición de los Likelihood Ratios:

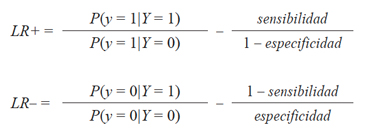
Podemos leer a cabalidad la siguiente salida de STATA:

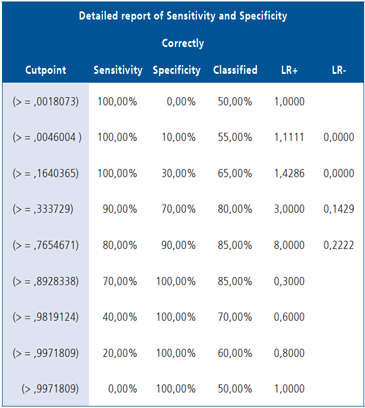
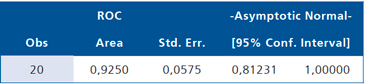
Si se ha escogido como punto de corte 0.7654671 el punto de corte para la variable original, X, se obtiene despejando su valor de la ecuación:

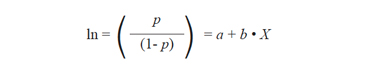
De donde:

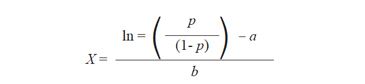
En nuestro caso:

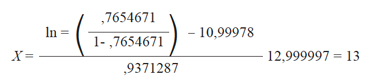
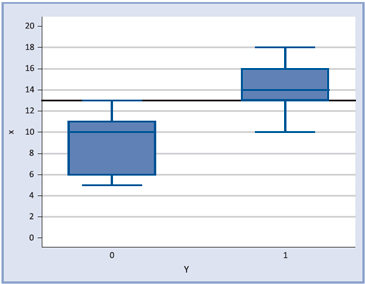
Obviamente, que conocido un desenlace, se puede utilizar una metodología idéntica, para evaluar un pronóstico.