Introducción a la Estadística
Gabriel Cavada Ch1
1División de Bioestadística, Escuela de Salud Pública, Universidad de Chile.
2Departamento de Salud Pública, Universidad de Los Andes.
La estadística llama estadígrafos o estadísticos a números resúmenes, que permiten establecer conclusiones acerca de la estructura de una muestra o de una colección de datos. Estos números son construidos considerando toda la información que contiene dicha muestra, es decir, se consideran todos los datos que han sido recolectados. Pueden construirse estadígrafos para distintos fines, sin embargo, estudiaremos tres tipos de ellos dado su amplio uso en la estadística descriptiva: estadígrafos de orden, de tendencia central y de variabilidad.
Cada vez que la muestra de datos, medidos al menos en escala ordinal, ha sido ordenada, es posible asignar a cada dato una ubicación (ranking) que indica su posición, en dirección ascendente, respecto al resto de la muestra. Esta ubicación se denota por un subíndice comprendido entre paréntesis. Por ejemplo, si se tienen los datos 12, 7, 15 y 13, al ordenarlos se tiene 7, 12, 13 y 15, es decir el primer dato de la ordenación es 7, el segundo 12, etc. Este hecho se expresa simbólicamente como sigue:
X(1)=7, X(2)=12, X(3)=13 y X(4)=15
Con esta notación, si se cuenta con n datos, el menor valor observado, que se llama el mínimo, será denotado por X(1) y el mayor valor observado, que se llama máximo, será denotado por X(n). La muestra se puede visualizar sobre un eje ordenado:

1. Estadígrafos de orden
Son aquellos que dan información acerca del orden en la estructura de una muestra. Ya se han mencionado dos de ellos que aparecen en forma instantánea al ordenar la muestra: el máximo, X(n), y el mínimo, X(1).
Se llama percentil a cada uno de los números que dividen la muestra en 100 partes iguales. En consecuencia, ellos son 99 y se denotan por P(k), donde k es el orden del percentil indicado. Dado el percentil P(k), éste divide la muestra en dos partes, la inferior que contiene el k% inferior de las observaciones y la superior que contiene el (100-k%) de las observaciones; entre dos percentiles consecutivos está contenido el 1% de la muestra. El siguiente esquema grafica las definiciones anteriores:
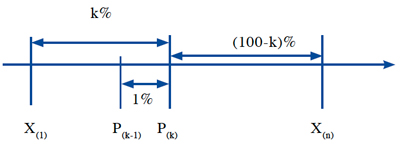
Hay percentiles que, por la popularidad de interpretación que tienen, reciben nombre propio. Entre ellos están:
- Los Cuartiles: son tres, denotados por Q1, Q2 y Q3, que corresponden respectivamente a los percentiles P25, P50 y P75 y que dividen la muestra en cuatro partes iguales.
- Los Quintiles: son cuatro, denotados por C1, C2, C3 y C4, que corresponden a los percentiles P20, P40, P60 y P80 y que dividen la muestra en cinco partes iguales.
- Los Deciles: son nueve, denotados por D1, D2,...,D9, que corresponden respectivamente a los percentiles P10, P20, ..., P90, y que dividen la muestra en diez partes iguales.
Un percentil de particular interés es el percentil cincuenta (P50) o Q2 o D5 que además recibe el nombre de mediana y divide la muestra en dos partes iguales.
1. Estadígrafos de tendencia central
Cada vez que se observa un fenómeno cuantitativo, interesa saber si los datos recolectados se aglutinan en torno a ciertos valores representativos que son propios del fenómeno estudiado. Por ejemplo, si se piensa en la Edad de los jugadores profesionales de fútbol, la experiencia dice que sus edades varían entre los 17 y 35 años, siendo raro, pero no imposible, encontrar jugadores con más de 35 o menores de 17 años; además, se sabe que la gran mayoría de estos jugadores tienen entre 23 y 30 años. Ahora la pregunta general se hace obvia, dada una colección de datos, ¿es posible saber a qué valores tienden dichos datos? La respuesta la entregan los llamados estadígrafos de tendencia central.
En consecuencia, se llaman estadísticos de tendencia central o de centralización a aquellos valores hacia los cuales tienden a aglomerarse los datos de una muestra. Los más utilizados son:
• La Moda. Es aquel valor que más se repite en una muestra y se denota por Mo. De suyo, la moda es el estadístico de centralización si la variable que se describe está medida en escala nominal. Como muestra la Tabla 1:
Tabla 1. Distribución por sexo.

Aquí “está de moda” ser de sexo femenino.
También la moda resulta ser un estadígrafo de fácil comprensión si la variable que se describe es de naturaleza ordinal o numérica pero discreta, como se ejemplifica en la Tabla 2:
Tabla 2. Distribución del número de hijos de mujeres post menopáusicas.
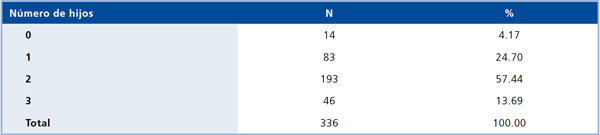
Aquí “está de moda” haber tenido dos hijos.
Si la variable es continua, formalmente la moda no existe, pues es muy difícil que al sacar una muestra de números reales dos o más de ellos coincidan. Por ejemplo, si se hilara fino y se midiera el peso de las personas en miligramos, sería muy poco probable encontrar dos o más personas con igual peso en una muestra; sin embargo, como generalmente el peso es medido en kilogramos enteros, en ese caso, como se ha discretizado la variable es posible calcularla. Sin embargo, aun así no es un buen estadígrafo de centralización.
La moda en una muestra podría no ser única, es decir, hay muestras bimodales o incluso multimodales.
• La Mediana. Es aquel valor que divide la muestra en dos partes iguales, como se dijo anteriormente. Debe notarse que la mediana es un estadígrafo de orden y también de centralización. (Ver Figura 1)
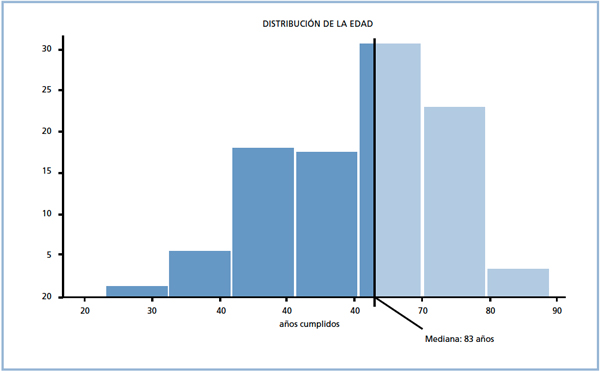
Figura 1. Representación de la mediana en un gráfico de distribución de la edad. El área clara y la oscura son iguales.
• La Media aritmética o Promedio aritmético. Es el estadígrafo de tendencia central más conocido, usado y abusado. Para todos es sabido que dada una colección de datos X1, X2, ...., Xn, el promedio se define como la suma de los datos dividida por la cantidad de datos, y se denota por; en símbolos el promedio es:
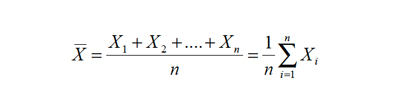
Formalmente, el promedio representa el Centro de Masas de la muestra; en la práctica, esto significa que se puede considerar que cada uno de los datos tiene valor igual al promedio. Cuando se calcula el promedio de edad de un grupo determinado de pacientes y éste es, por ejemplo, 62 años, se debe entender que todos los pacientes tienen aproximadamente 62 años. Para que esta conclusión esté de acuerdo con la realidad, se debe puntualizar que esto ocurre en dos situaciones que podrían darse juntas o por separado:
a) Cuando la muestra es homogénea, es decir los datos son parecidos entre sí. Suponga que las calificaciones escolares en matemáticas de un alumno son: 3.8; 3.8; 3.9; 4.1; 4.2 y 4.2, es fácil observar que estas calificaciones tienen promedio 4.0 y no se comete un error grave si se reporta que cada una de las notas fueron igual a 4.0.
b) La muestra tiene valores extremos compensados, es decir la muestra es simétrica. Suponga ahora que las notas de nuestro alumno son: 1.0; 3.8; 3.8; 3.9; 4.1; 4.2; 4.2 y 7.0; también este conjunto tiene promedio 4.0 pero además se debe aceptar que tanto el 1.0 como el 7.0 son “accidentes” en las calificaciones, por lo tanto no se comete un grave error al comunicar que este alumno tiene un rendimiento de 4.0.
Las situaciones anteriores se pueden observar en la Figura 2:
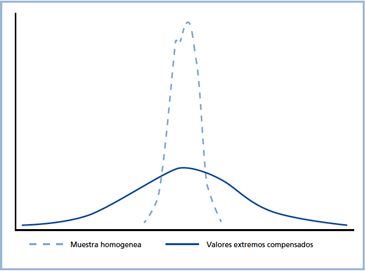 Figura 2. Representación de la distribución de una muestra homogénea y otra heterogénea
Figura 2. Representación de la distribución de una muestra homogénea y otra heterogénea
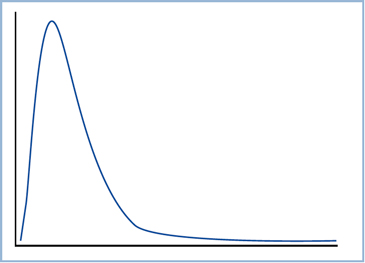 .Figura 3. Representación de una distribución asimétrica.
.Figura 3. Representación de una distribución asimétrica.
Un error muy frecuente es describir el promedio de una variable ordinal; por ejemplo, en la literatura es frecuente encontrar que “la intensidad del dolor se ha medido a través de la escala EVA y basalmente se encontró un promedio de dolor igual a 7.3”. El error es garrafal puesto que la escala EVA es ordinal y además no es posible asimilar la intensidad de dolor 7.3.
Cuando la distribución de los datos es asimétrica o cuando la escala de medida es ordinal el estadístico de centralización mas apropiado es la mediana.
2. Estadígrafos de variabilidad o dispersión
Acabamos de ejemplificar una situación en que los datos analizados no son homogéneos; cuando se cuenta con pocos datos, por simple inspección sabríamos si los datos son homogéneos o heterogéneos. Sin embargo, resulta extremadamente útil manejar medidas para la variabilidad, con el objeto de establecer comparaciones posteriores. Consideremos las calificaciones en estadística de dos alumnos: Pedro y Pablo.

Como se observa, tanto Pedro como Pablo tienen idéntico rendimiento promedio. Sin embargo ¿quién tiene rendimiento más homogéneo?, por inspección vemos que Pedro, pues obtuvo sólo notas 4.0, mientras que Pablo obtuvo toda la gama de calificaciones. Para contestar la pregunta propuesta mediante el uso de indicadores estadísticos se desarrollaron los Estadígrafos de Variabilidad. Aquí presentaremos sólo tres de ellos:
• Rango o Recorrido. Se define el rango o recorrido de los datos como el máximo menos el mínimo, lo que en símbolos se expresa así:
Rango = X(n) - X(1)
En nuestro ejemplo, Rango (Pablo)=6 y Rango (Pedro)=0. Observamos que mientras más heterogénea es la colección de datos mayor es el valor del rango. Sin embargo, el Rango puede exagerar el grado de heterogeneidad de los datos; para prevenir este hecho se prefiere usar como medida de variabilidad la conocida como:
• Rango Intercuartílico. Es la diferencia entre el tercer y primer cuartil:
RIC = Q3 -Q1
Nos permite ubicar a la mediana con respecto a éstos cuartiles. El primer cuartil (Q1) deja al 25% de los datos por debajo de él y el tercer cuartil (Q3) deja al 75%; por lo tanto, entre ambos cuartiles se encuentra el 50% de los datos.
Cuando una muestra no presenta distribución simétrica, para lograr una aproximación de la distribución de los datos se recomienda tener un resumen de 5 estadígrafos: el valor mínimo, el primer cuartil, la mediana, el tercer cuartil y el valor máximo.
• Desviación Estándar. Para definir la desviación estándar, previamente presentaremos lo que se llama desviación de un dato respecto al promedio, que denotamos por “di”:
d = X1 - X
Es decir señala la diferencia entre cada dato y el promedio. La suma de los desvíos es siempre cero, por ello para construir un estadígrafo de variabilidad basado en los desvíos y por las propiedades matemáticas se prefiere hacerlo sobre los desvíos elevados al cuadrado.
En consecuencia definimos la Desviación Estándar, denotada por “Sx o σx” como:
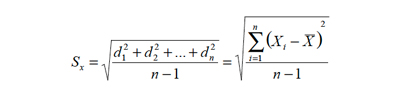
Así, siguiendo el ejemplo anterior:
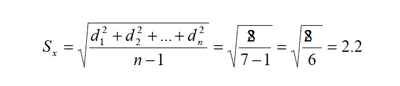
La interpretación de la desviación estándar, bajo ciertas condiciones de regularidad, como la simetría de los datos y un apuntamiento moderado de su histograma, es que “la mayoría de éstos se encuentra entre el Promedio Menos la Desviación y el Promedio Más la Desviación”, lo que en el ejemplo dado resulta en que las notas de Pablo están entre 4 - 2.2 y 4 + 2.2, es decir entre 1.8 y 6.2, lo que es bastante real.
Solamente para obtener una medida más interpretable del grado de heterogeneidad, es útil definir el Coeficiente de Variabilidad que se entrega como un valor porcentual y se define como el cuociente entre la desviación estándar y el promedio multiplicado por 100 en símbolos:
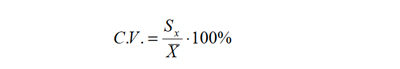
Para nuestro ejemplo:
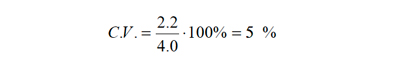
es decir un 55% de variabilidad, lo que es moderadamente alto y señala que los datos presentan gran dispersión.
Un problema o limitante del coeficiente de variabilidad es que podría presentar un valor muy alto debido a que el promedio de los datos es cercano a cero y no debido a la heterogeneidad de éstos.
• Varianza. Si bien la varianza es el cuadrado de la desviación estándar, ella constituye la medida más utilizada para describir la dispersión de datos continuos. En el caso anterior tiene valor:
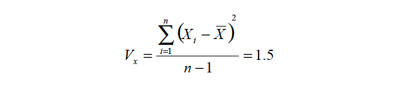
Como medidas de variabilidad más importantes, conviene destacar algunas características de la varianza y la desviación estándar:
- Son medidas que describen la variabilidad o dispersión y por tanto cuando los datos están muy alejados de la media, el numerador de sus fórmulas será grande y la varianza y la desviación estándar también lo serán.
- Al aumentar el tamaño de la muestra, disminuye la varianza y la desviación estándar.
- Cuando todos los datos de la distribución son iguales, la varianza y la desviación estándar son iguales a 0.
- Para su cálculo se utilizan todos los datos de la distribución; por tanto, cualquier cambio de valor será detectado.