Variables aleatorias: El caso continuo
Gabriel Cavada Ch.1
1División de Bioestadística, Escuela de Salud Pública, Universidad de Chile.
El tratamiento de una variable aleatoria continua es matemáticamente más complejo que el de una variable aleatoria discreta, debido a la completitud de los números reales, lo que significa que cualquier subconjunto de números reales tiene infinitos elementos y sus elementos no son enumerables; en consecuencia, si consideramos una variable de naturaleza continua, como por ejemplo el peso de una persona adulta, de sexo femenino y sana, que en una determinada población la podríamos situar entre los 40 y 70 kilógramos, es obvio asumir que una persona incluida en esta población, puede tener como peso cualquier valor comprendido en la dispersión dada. Si pensamos en el experimento consistente en “extraer una persona al azar y pesarla” y definimos el suceso A: “la persona pesa exactamente 48 kilógramos”, entonces la P(A) = 0, ya que se trata de escoger un solo valor de un espacio muestral que tiene infinitos elementos. Este hecho nos lleva a renunciar a calcular la probabilidad de un evento como A, en cambio, nos podemos preguntar por la probabilidad del siguiente evento: B: “la persona escogida pesa entre 50 y 55 kilógramos”, es claro que si contáramos con evidencia empírica, es decir con datos, que pudiésemos graficar, la estimación de la probabilidad del evento B, sería el área más oscura en la Figura 1.
Esta área es aproximadamente el 41% del total, es decir P(B) = 0,41; pues bien, si quisiéramos formalizar esta idea, tendríamos que conocer la función matemática en cuyo trazado se circunscribe el histograma mostrado en la Figura 1, es decir, deberíamos conocer la expresión matemática de la función mostrada en la Figura 2 y calcular el área destacada.
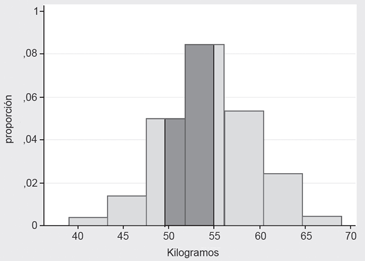 Figura 1
Figura 1
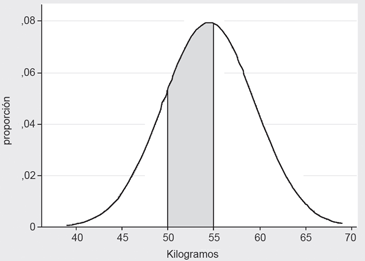 Figura 2
Figura 2
La funcion a la que hacemos referencia recibe el nombre de gfuncion densidad de probabilidadesh, que abreviaremos como fdp. Una funcion, f(x), es una fdp si cumple con dos condiciones:
i. Es una funcion no negativa, es decir f (x) . 0, para cualquier valor de x.
ii. El area total que ella encierra bajo su grafico y el eje x es igual a 1. En simbolos: 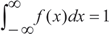
Gráficamente:
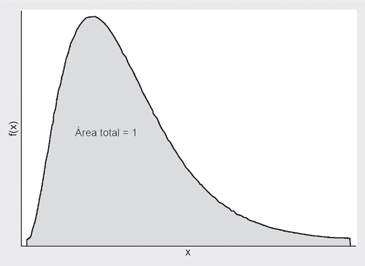 Figura 3.
Figura 3.
En estas condiciones, es posible calcular la probabilidad de que la variable X se encuentre entre los valores a y b; en símbolos:
![]()
O sea, el área que encierra f(x) entre las verticales X = a y X = b:
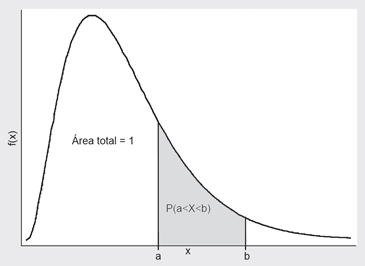 Figura 4.
Figura 4.
Se define la función de distribución de probabilidades (fdp) como:
![]()
Es decir la fdp cuantifica el área acumulada bajo la fdp hasta el punto x, como muestra la siguiente Figura 5:
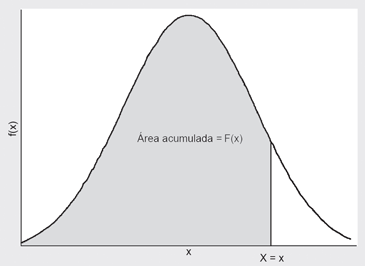 Figura 5.
Figura 5.
Se observa que F (X) es acotada, ya que, 0 . F(X) . 1 y que F(X) es siempre una funcion creciente, como muestra la Figura 6:
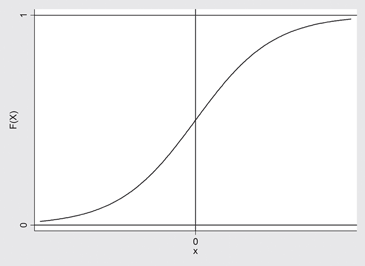 Figura 6.
Figura 6.
Así:
![]()
Notar que:
![]()
Ya que P (X = a) = P (X = b) = 0.
Caracterización de una variable aleatoria contínua
Dada una función densidad de probabilidades se define la Esperanza matemática o valor esperado de la variable X a la expresión:
![]()
El momento de orden 2 está dado por la expresión:
![]()
Expresiones que permiten calcular la varianza de la variable X, a través de la expresión:
![]()
Algunas distribuciones de probabilidad contínua
La distribución uniforme, X~U[a,b]
La variable X sigue una distribución uniforme en el intervalo [a,b], si su fdp es:
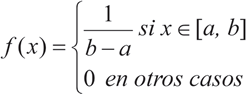
Cuyo gráfico, en el caso de la U[1,5] es:
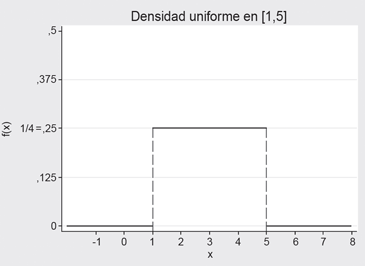 Figura 7.
Figura 7.
La función de distribución de probabilidades es:
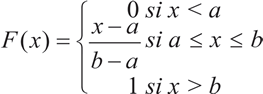
El gráfico de la fdp, en el caso de la U[1,5] es:
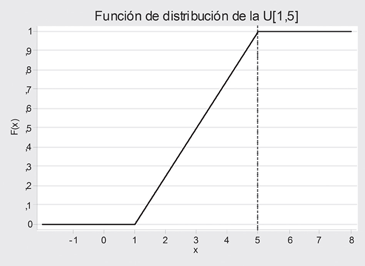 Figura 8.
Figura 8.
La esperanza y la varianza son:
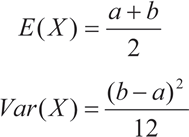
Ejemplo: Una persona llega en forma aleatoria entre las 12:00 y las 12:15 horas a una determinada estación de Metro. Si un tren pasa exactamente a las 12:00 horas y los trenes tienen una frecuencia de 5 minutos. Calcular la probabilidad de que la persona espere más de 2 minutos un tren.
Si t es la variable tiempo de espera, en minutos, t~U[0,15], esta fdp la representamos gráficamente así:
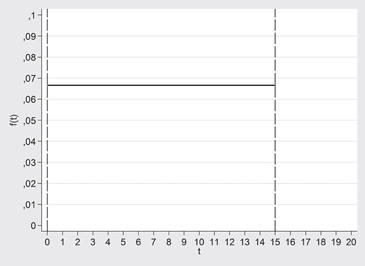 Figura 9.
Figura 9.
Luego, las áreas amarillas indican cuando ocurre el suceso de interés:
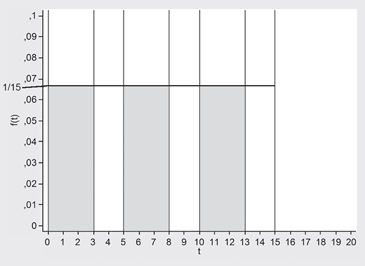 Figura 10.
Figura 10.
En consecuencia, si A es el evento de esperar más de 2 minutos un tren:
![]()
La distribución exponencial, X~exp(α)
Una importante distribución de probabilidades de una variable continua es la llamada distribución exponencial, que es la base para el análisis de sobrevida.
La variable X sigue una distribución exponencial de parámetro α si su fdp es:
![]()
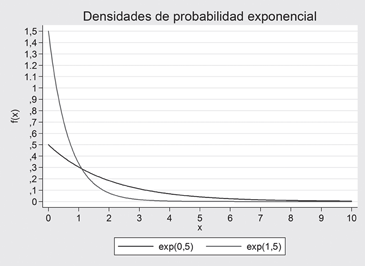 Figura 11.
Figura 11.
La función de distribución de probabilidades es:
![]()
El gráfico de la fdp, en el caso de la exp(0,5) es:
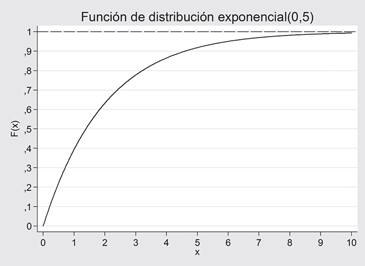 Figura 12.
Figura 12.
La esperanza y la varianza son:
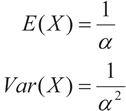
Ejemplo: Se sabe que el tiempo de duración de un
marcapasos sigue una distribución exponencial. En base a
registros de una serie de casos, se ha encontrado que en
promedio, estos marcapasos han durado 60 meses. Calcular
la probabilidad de que un marcapasos dure menos de 6 años:
Llamando x al tiempo de duración de un marcapasos, se tiene que E[x] = 60, con lo que α = 1/60, así la ftp para x es:
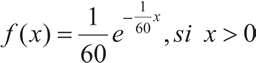
con lo que la ftp es
![]()
Con lo que la probabilidad de que el marcapasos dure menos de 6 años es:
![]()
La distribución Normal o Gausstiana, X~N(μ,σ2)
Sea X una variable continua con recorrido R; diremos que X tiene una distribucion normal (o gaussiana) si su fdp es:
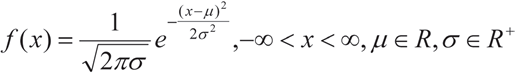
El gráfico de la densidad N(μ,σ2) es una curva tal que:
a) tiene máximo absoluto en x = μ
b) es simétrica respecto a la vertical x = μ
c) tiene puntos de inflexión en x = μ - σ y x = μ + σ
d) se aproxima asintóticamente al eje de abscisas, lo
que se refleja en la relación
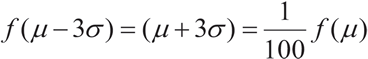
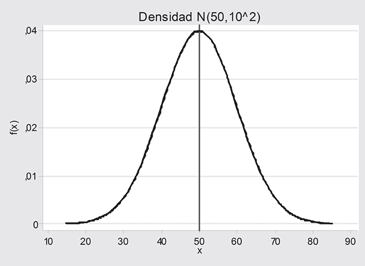 Figura 13.
Figura 13.
La esperanza y la varianza son:
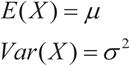
La distribución normal estándar o típica
Si z~N(0,1) se habla de la distribución normal estándar o típica, así:
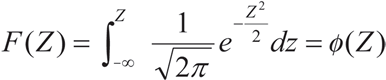
función que se encuentra tabulada.
Estandarización de variables aleatorias normales
La estandarización de una variable aleatoria normal, es la transformación de dicha variable en una variable con distribución normal estándar, este proceso se obtiene usando el siguiente teorema:
Si X~N(m,s2) entonces 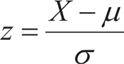 ~N(0,1)
~N(0,1)
Al valor de z se le llama puntaje típico y representa la
distancia de X a su promedio en unidades de desviación
estándar.
En consecuencia, al estudiar la distribución normal
estándar, se pueden generalizar algunas cosas de interés,
como las probabilidades que se muestran en la Figura 14:
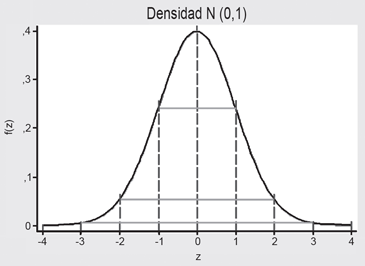 Figura 14.
Figura 14.
Es decir, la probabilidad de encontrarse en torno al promedio en ± 1 desviación estándar es 68,3%, ± 2 desviaciones estándar es 95,5% y en ± 3 desviaciones estándar es 99,3%. Este resultado permite tener una respuesta aproximada a la interrogante si una colección de datos tiene una distribución normal.
Algunos percentiles clásicos de la normal estándar:
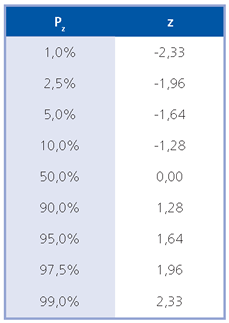
Propiedades de la distribución normal
Algunas propiedades de la distribución normal son las
siguientes:
a) Si X ~N(μ,σ2) → Y= a+b·X ~ N (a+b·μ,b2 σ2)
b) Si X ~N (μx ,σ2 x) e Y ~N (μy ,σ2y) y además X
independiente de Y → X±Y ~N (μx ± μy,σ2x + σ2y)
c) Si son independientes tales que Xi ~N (μi,σ2 i) →![]()
d) Si son independientes e idénticamente distribuidos N
(μ,σ2) →![]() N (nμ,nσ2)
N (nμ,nσ2)
Tal vez uno de los resultados más notables de la estadística, sea el conocido Teorema Central del Límite, cuyo enunciado es:
Si ![]() son independientes e idénticamente distribuidas
tales que E [X] = μ y Var [X]= σ2 →
son independientes e idénticamente distribuidas
tales que E [X] = μ y Var [X]= σ2 → ![]() N(nμ,nσ2) cuando
N(nμ,nσ2) cuando![]() . Este teorema también se puede enunciar
del siguiente modo:
. Este teorema también se puede enunciar
del siguiente modo:
Si ![]() son independientes e idénticamente distribuidas
tales que E [X] = μ y Var [X]= σ2 →
son independientes e idénticamente distribuidas
tales que E [X] = μ y Var [X]= σ2 → 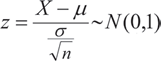 cuando
n → ∞. Este teorema es básico para construir la inferencia
estadística paramétrica.
cuando
n → ∞. Este teorema es básico para construir la inferencia
estadística paramétrica.
La distribución normal, es la distribución más usada y
abusada por el usuario de la estadística. La forma de
la clásica campana de Gauss, nos da la idea común de
normalidad, esto es “ni mucho ni poco”, sin embargo la
normalidad estadística no siempre coincide con el concepto
de normalidad clínica.
La Figura 15, muestra la diferencia distributiva del índice
de masa corporal estandarizado (referencia CDC 2000) de
un grupo de escolares chilenos respecto a la distribución
teórica que es la normal estándar. Se puede deducir que
este grupo de niños es aproximadamente 2 desviaciones
estándar más obeso que la referencia:
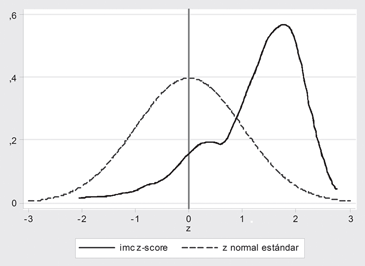 Figura 15
Figura 15