Cálculo de probabilidades. Primera parte

Introducción

El cálculo de probabilidades se origina en la época post renacentista, fruto del estudio de los juegos de azar, por el deseo de cuantificar las posibilidades de ganar o perder ante una baza de naipes, el lanzamiento de un dado o de una moneda al aire. Este interés lúdico inicial trascendió en la historia del pensamiento, pues el análisis fino de cualquier situación real lleva a considerar la porción de azar (imponderable) presente en la misma. Tanto es así que la única seguridad que tenemos es nuestra muerte “biológica”. Cuando decimos que algo será “seguro” en realidad estamos diciendo que es altamente probable que ello ocurra.

En el estudio de la realidad se distinguen dos tipos de experimentos: los deterministicos y los probabilisticos:

1) Los experimentos deterministicos son aquellos que tienen solo un resultado posible y, ademas, este es predecible. Por ejemplo, si el experimento consiste en soltar una piedra desde una cierta altura y observar el sentido del movimiento, el unico resultado posible sera que la piedra caiga en la direccion vertical y hacia el suelo.

2) Los experimentos probabilisticos son aquellos que tienen mas de un resultado posible y cada resultado es impredecible. Por ejemplo, lanzar una moneda al aire y observar que lado mostrara despues de caer. Notemos que si bien sabemos de antemano que la moneda puede mostrar gcarah o gselloh, no podemos predecir que ocurrira y el resultado lo conoceremos solo despues que la moneda haya finalizado su movimiento.

Dado un experimento cualquiera, que llamaremos E, definimos como ESPACIO MUESTRAL, denotado por Ω, al conjunto de todos los posibles resultados de E. Como ejemplos tenemos:

a) E: Se lanza una moneda al aire
    Ω={cara, sello}
b) E: Se lanza un dado
    Ω={1,2,3,4,5,6}

Se llama suceso o evento a cualquier subconjunto de Ω, los que se identifican por letras mayúsculas. El hecho que A sea un suceso de Ω, lo denotamos por A⊂Ω. Observamos inmediatamente que el conjunto vacío (Ø) es un suceso, pues Ø⊂Ω y le llamamos suceso vacío o suceso imposible.

Si jugamos al “cara” o “sello” y previamente se nos pregunta por la “probabilidad” de sacar cara, diremos que es 50%, pues hay sólo dos posibles resultados, pero además hemos supuesto que las posibilidades de obtener cara son idénticas a las de obtener sello, concepto que se denomina EQUIPROBABILIDAD. En lenguaje técnico diremos que los resultados, cara y son equiprobables, obviamente si es que la moneda que se lanza no está cargada.

Se llama medida de un conjunto a algún número que nos indique el tamaño del conjunto; así, la medida del conjunto A se denota por m(A). Si el conjunto es finito y se pueden contar sus elementos, la medida natural que aparece es m(A)= “número de elementos del conjunto”. Por ejemplo si Ω={1,2,3,4,5,6} entonces m(Ω)=6.

Si el conjunto es un intervalo de la recta real o una porción del plano cartesiano puede considerarse como m(A)= “longitud del intervalo” o m(A)= “área de la porción del plano cartesiano” según sea el caso.

- Definición clásica de probabilidad, probabilidad de la unión, sucesos excluyentes, probabilidad condicional, probabilidad total y fórmula de Bayes.

Introducido el concepto de medida, podemos definir la probabilidad de un suceso A como: “medida de A dividida por medida de Ω”. En símbolos:

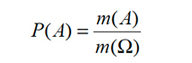
De esta definición aparecen dos resultados fundamentales:
P(Ø)=0, la probabilidad del suceso imposible es nula.
P(Ω)=1, la probabilidad del espacio muestral es 1.
Dos sucesos A y B se dicen excluyentes, si es IMPOSIBLE que ocurran al mismo tiempo; en símbolos A∩B=Ø. Por
ejemplo si al lanzar un dado, éste muestre “un número par e impar” a la vez.

Hechas las consideraciones anteriores, enunciamos los AXIOMAS del cálculo de probabilidades:

a) 0 ≤ P(A) ≤ 1
b) Para una colección de sucesos excluyentes: P(E1∪E2U…UEn)=P(E1)+P(E2)+…+ P(En)

Para enfrentar un problema de cálculo de probabilidades, se deben definir cuidadosamente los sucesos de interés. Ejemplifiquemos con algunas situaciones elementales como el experimento de “lanzar un dado”:

E:  Se lanza un dado
     Ω={1,2,3,4,5,6}

Definamos los sucesos siguientes y calculemos sus probabilidades de ocurrencia

A: “el dado muestra 1”, así: A=1 y m(A)=1, con lo que:

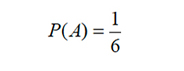
B: “el dado muestra un número impar”, así B={1,3,5} y m(B)=3, con lo que:

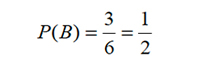
Sin embargo, la realidad presenta sucesos compuestos que se forman por unión, intersección y complementación. Efectuemos estas composiciones y estudiemos su significado. En consecuencia, dados los sucesos A y B se tiene:

A∩B: sucede A y sucede B (ambos a la vez)
A∪B: sucede A ó B, así: P(A ∪B)=P(A) + P(B) – P(A∩ B)
Ac: no sucede A, así P(Ac)=1 – P(A)

Decimos que los sucesos A y B son INDEPENDIENTES, si la ocurrencia de uno de ellos no altera la ocurrencia o no ocurrencia del otro; la hipótesis de independencia se expresa así: P(A∩ B) = P(A)P(B).

Además, la realidad presenta abundantes SUCESOS CONDICIONALES, es decir, aquellos que condicionan su ocurrencia a la presencia de otros. Por ello, podemos preguntar por la probabilidad de que ocurra un evento DADO EL HECHO que ocurrió tal o cual otro evento. Si consideramos los sucesos A y B, de modo que B condiciona la ocurrencia de A, entonces la probabilidad de que “ocurra A dado el hecho que ocurrió B” es:

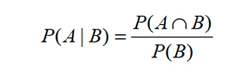
Nota: En la realidad es difícil acceder a la P(A∩B), sin embargo, se puede disponer de P(A|B) y P(B), luego hay que tener presente que P(A∩B)=P(A|B) P(B).

En múltiples oportunidades la ocurrencia de un suceso principal A se debe a la ocurrencia previa de causas, que también son sucesos, de modo que en el cálculo de la probabilidad de la ocurrencia de A las probabilidades de los sucesos causales deben ser incluidas según la ponderación o influencia que tengan sobre A. Si el suceso principal A se debe a las causas E1, E2,..., En , entonces:

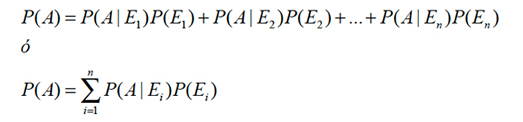
Esta fórmula recibe el nombre de TEOREMA DE LA PROBABILIDAD TOTAL.

Consideremos ahora el problema de calcular la probabilidad de que el suceso principal A se haya producido debido a la causa Ek . En símbolos buscamos P(Ek|A) y este resultado es simple de encontrar, pues proviene de:

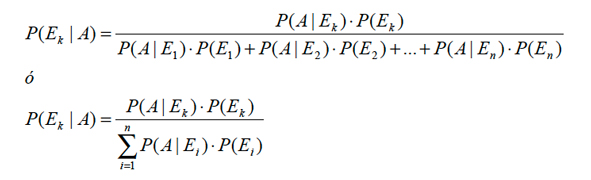
Esta fórmula es conocida como el TEOREMA DE BAYES, donde el denominador no es más que la probabilidad total.

Ejemplo: En un hospital hay tres servicios: Urgencia, Cirugía y Medicina. El porcentaje de hospitalizados por servicio es: Urgencia 30%, Cirugía 20% y Medicina 50%. Si la mortalidad en cada servicio es 10%, 5% y 3%, respectivamente. ¿Cuál es la probabilidad de que un paciente hospitalizado muera?

Suceso principal, A : el paciente muere

Causas:  E1: el paciente está en urgencia
               E2: el paciente está en cirugía
               E3: el paciente está en medicina

       P(A) = 0.1·0.3 + 0.05·0.2 + 0.03·0.5 = 0.055

Y si se nos comunica que ha ocurrido una muerte, ¿Cuál es la probabilidad que haya ocurrido en Urgencia?

Suceso principal, A: el paciente muere

Causas:  E1: el paciente está en urgencia
               E2: el paciente está en cirugía
               E3: el paciente está en medicina

Es decir se pide:

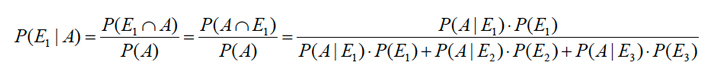
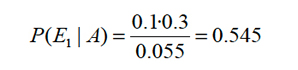
Una situación clásica es lo que ocurre con los exámenes diagnósticos, cuyos resultados se cruzan con la verdadera situación del paciente. Es decir, se distinguen los sucesos: “El paciente está sano”, “El paciente está enfermo”, “El examen da positivo” y “El examen da negativo”; la situación la observamos en la siguiente tabla:

Así:

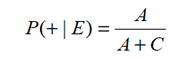 ,recibe el nombre de sensibilidad del examen

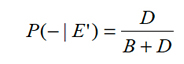 ,recibe el nombre de especificidad del examen

Falsos positivos son aquellos sanos cuyo examen da positivo; falsos negativos son aquellos enfermos cuyo examen da negativo.

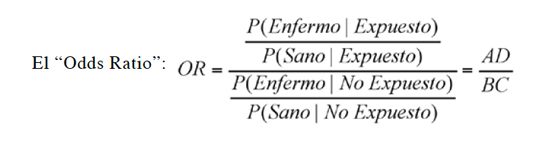
Una configuración similar a la anterior es usada comúnmente en epidemiología, pues el sujeto se clasifica doblemente, según una respuesta (enfermo o sano) y una variable explicativa (expuesto o no expuesto), así:

Así es posible calcular P(Enfermo|Expuesto), P(Sano|Expuesto), P(Enfermo|No expuesto) y P(Sano|No expuesto) y como medidas de la asociación se proponen:

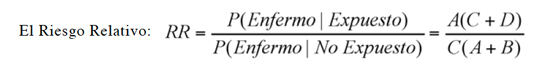
Ambas medidas de asociación tienen valor de nulidad igual a 1, es decir si RR u OR son 1 significa que no hay asociación entre enfermedad y exposición.

El riesgo relativo sólo se puede calcular en diseños transversales o prospectivos, ya que siempre los totales de exposición o no exposición no son aleatorios, mientras que el OR se puede calcular en diseños transversales, prospectivos y retrospectivos; además, el OR tiene propiedades matemáticas muy deseables lo que lo hacen una medida de asociación más universal.

Si el número relativo de enfermos es pequeño (prevalencia baja) RR y OR son numéricamente similares.

Tradicionalmente si RR u OR es menor que 1 se habla que la exposición es un factor protector, mientras que si son mayores que 1 se habla de un factor de riesgo. Las inferencias estadísticas asociadas a estos indicadores se verán en un artículo futuro.